ダイスを複数振ったときの出目の合計について、任意の出目dが出る確率を求めようと思う。
古来からの習慣に従って、n個の6面ダイスを振った合計をnD6と表記する。
当然だが、ダイスを投げたとき、それぞれの目の出る事象は同様に確からしいとする。
2D6
例示は理解の試金石ということだし、まず2D6について考える。
各出目が出る確率は次の通りとなる。
| 2 | 1/36 |
| 3 | 2/36 |
| 4 | 3/36 |
| 5 | 4/36 |
| 6 | 5/36 |
| 7 | 6/36 |
| 8 | 5/36 |
| 9 | 4/36 |
| 10 | 3/36 |
| 11 | 2/36 |
| 12 | 1/36 |
分母の36を無視してこれをグラフに表記すると次のようになる。
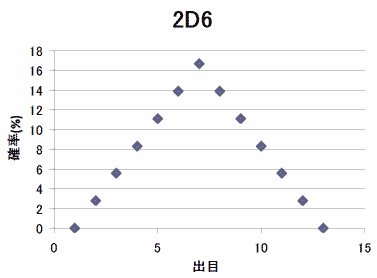
見ての通り、簡単な式で表せそうな形をしているので、式を書き出してみる。
y=-|x|が原点で折り返す上に凸な三角のグラフになるから、コイツをx軸方向に7、y軸方向に6移動すればよいので、(y-6)=-|x-7|となって、これを整理すると・・・、などと考えながら解は得られる。
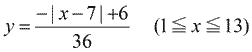
となる。実に簡単ではないか。
3D6
2D6があっさり解決したので調子に乗って3D6についてもやってみる。
3D6は63=216の組み合わせがあるので確率を書き出すのは結構大変だった。
| 3 | 1/36 |
| 4 | 3/36 |
| 5 | 6/36 |
| 6 | 10/36 |
| 7 | 15/36 |
| 8 | 21/36 |
| 9 | 25/36 |
| 10 | 27/36 |
| 11 | 27/36 |
| 12 | 25/36 |
| 13 | 21/36 |
| 14 | 15/36 |
| 15 | 10/36 |
| 16 | 6/36 |
| 17 | 3/36 |
| 18 | 1/36 |
2D6のときと同様に、分母の216を無視してこれをグラフに表記すると次のようになる。
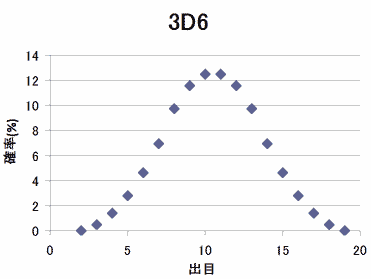
正規分布じみたラインが得られた。これは、このままダイスを増やしていくと正規分布に近づいていくんだろうと予測が付く。ちなみに、正規分布から確率を表そうという試みもしたが、好ましい結果は得られなかったので割愛する。興味があったら下の方で公開するエクセルファイルにそれらしい残滓があるので見てもらうとよい。
こうして、3D6の確率分布が得られたが、法則性が見えそうで見えない。
続く4D6以降を見てみたら、何か気付くところがあるだろうか、と計算してみることにする。
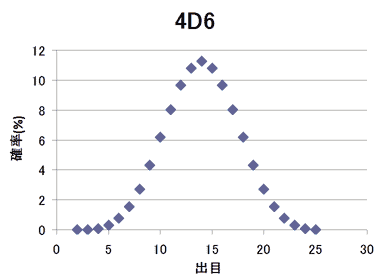
4D6
64=1296ということで、さすがに手で計算するには骨が折れるのでエクセルで数えることにした。方法としては1296を4桁の6進数で数えて、各桁に1を足したものをダイス目と考えて、その合計値がそれぞれ何個あるかを数えるという方法。
| 4 | 1/1296 |
| 5 | 4/1296 |
| 6 | 10/1296 |
| 7 | 20/1296 |
| 8 | 35/1296 |
| 9 | 56/1296 |
| 10 | 80/1296 |
| 11 | 104/1296 |
| 12 | 125/1296 |
| 13 | 140/1296 |
| 14 | 146/1296 |
| 15 | 140/1296 |
| 16 | 125/1296 |
| 17 | 104/1296 |
| 18 | 80/1296 |
| 19 | 56/1296 |
| 20 | 35/1296 |
| 21 | 20/1296 |
| 22 | 10/1296 |
| 23 | 4/1296 |
| 24 | 1/1296 |
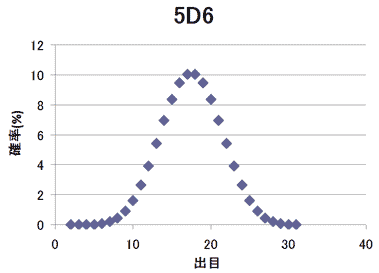
5D6
| 5 | 1/7776 |
| 6 | 5/7776 |
| 7 | 15/7776 |
| 8 | 35/7776 |
| 9 | 70/7776 |
| 10 | 126/7776 |
| 11 | 205/7776 |
| 12 | 305/7776 |
| 13 | 420/7776 |
| 14 | 540/7776 |
| 15 | 651/7776 |
| 16 | 735/7776 |
| 17 | 780/7776 |
| 18 | 780/7776 |
| 19 | 735/7776 |
| 20 | 651/7776 |
| 21 | 540/7776 |
| 22 | 420/7776 |
| 23 | 305/7776 |
| 24 | 205/7776 |
| 25 | 126/7776 |
| 26 | 70/7776 |
| 27 | 35/7776 |
| 28 | 15/7776 |
| 29 | 5/7776 |
| 30 | 1/7776 |
6D6
| 6 | 1/46656 |
| 7 | 6/46656 |
| 8 | 21/46656 |
| 9 | 56/46656 |
| 10 | 126/46656 |
| 11 | 252/46656 |
| 12 | 456/46656 |
| 13 | 756/46656 |
| 14 | 1161/46656 |
| 15 | 1666/46656 |
| 16 | 2247/46656 |
| 17 | 2856/46656 |
| 18 | 3431/46656 |
| 19 | 3906/46656 |
| 20 | 4221/46656 |
| 21 | 4332/46656 |
| 22 | 4221/46656 |
| 23 | 3906/46656 |
| 24 | 3431/46656 |
| 25 | 2856/46656 |
| 26 | 2247/46656 |
| 27 | 1666/46656 |
| 28 | 1161/46656 |
| 29 | 756/46656 |
| 30 | 456/46656 |
| 31 | 252/46656 |
| 32 | 126/46656 |
| 33 | 56/46656 |
| 34 | 21/46656 |
| 35 | 6/46656 |
| 36 | 1/46656 |
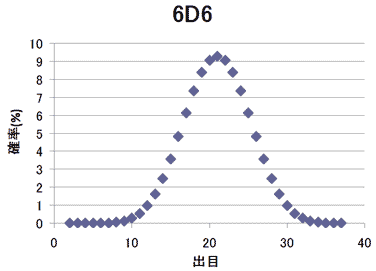
6D6だと、66=46656となり、これを数えるのはエクセルでも辛くなってくる。46656マス並べて数えなければならないので、ファイル容量も大変なものになってくるので愚直に数えるのはここまでとする。
さて、2D6から6D6まで並べてみたわけだが、3D6で予想したように正規分布に近づいてくることは分かった。というか、正規分布の定義上近づいてくるのは当然なのだが、正規分布の方から確率を逆算する試みはうまくいかなかった。
仕方がないので、数列として調べて法則性を探すことにする。
とはいっても、数列とかそんなに得意なわけでもないので、できることといったら階差数列になっているか調べるくらいしかない。ただ、階差を調べるだけでは芸がないので、法則性が見つかるまで階差をとり続けてみることにする。HTMLだと行間に差分を表示するのが難しいので、上の数字との差を横のマスに書くことにする。また、分母の部分は6nということで始めから規則性が分かっているので省く。
ということで2D6から順に見ていく。
2D6
| 出目 | 個数 | 差 |
| 1 | 0 | 0 |
| 2 | 1 | 1 |
| 3 | 2 | 1 |
| 4 | 3 | 1 |
| 5 | 4 | 1 |
| 6 | 5 | 1 |
| 7 | 6 | 1 |
| 8 | 5 | -1 |
| 9 | 4 | -1 |
| 10 | 3 | -1 |
| 11 | 2 | -1 |
| 12 | 1 | -1 |
| 13 | 0 | -1 |
| 14 | 0 | 0 |
3D6
| 出目 | 個数 | 差 | 差 |
| 2 | 0 | 0 | 0 |
| 3 | 1 | 1 | 1 |
| 4 | 3 | 2 | 1 |
| 5 | 6 | 3 | 1 |
| 6 | 10 | 4 | 1 |
| 7 | 15 | 5 | 1 |
| 8 | 21 | 6 | 1 |
| 9 | 25 | 4 | -2 |
| 10 | 27 | 2 | -2 |
| 11 | 27 | 0 | -2 |
| 12 | 25 | -2 | -2 |
| 13 | 21 | -4 | -2 |
| 14 | 15 | -6 | -2 |
| 15 | 10 | -5 | 1 |
| 16 | 6 | -4 | 1 |
| 17 | 3 | -3 | 1 |
| 18 | 1 | -2 | 1 |
| 19 | 0 | -1 | 1 |
| 20 | 0 | 0 | 1 |
| 21 | 0 | 0 | 0 |
4D6
| 出目 | 個数 | 差 | 差 | 差 |
| 3 | 0 | 0 | 0 | 0 |
| 4 | 1 | 1 | 1 | 1 |
| 5 | 4 | 3 | 2 | 1 |
| 6 | 10 | 6 | 3 | 1 |
| 7 | 20 | 10 | 4 | 1 |
| 8 | 35 | 15 | 5 | 1 |
| 9 | 56 | 21 | 6 | 1 |
| 10 | 80 | 24 | 3 | -3 |
| 11 | 104 | 24 | 0 | -3 |
| 12 | 125 | 21 | -3 | -3 |
| 13 | 140 | 15 | -6 | -3 |
| 14 | 146 | 6 | -9 | -3 |
| 15 | 140 | -6 | -12 | -3 |
| 16 | 125 | -15 | -9 | 3 |
| 17 | 104 | -21 | -6 | 3 |
| 18 | 80 | -24 | -3 | 3 |
| 19 | 56 | -24 | 0 | 3 |
| 20 | 35 | -21 | 3 | 3 |
| 21 | 20 | -15 | 6 | 3 |
| 22 | 10 | -10 | 5 | -1 |
| 23 | 4 | -6 | 4 | -1 |
| 24 | 1 | -3 | 3 | -1 |
| 25 | 0 | -1 | 2 | -1 |
| 26 | 0 | 0 | 1 | -1 |
| 27 | 0 | 0 | 0 | -1 |
| 28 | 0 | 0 | 0 | 0 |
5D6
| 出目 | 個数 | 差 | 差 | 差 | 差 |
| 4 | 0 | 0 | 0 | 0 | 0 |
| 5 | 1 | 1 | 1 | 1 | 1 |
| 6 | 5 | 4 | 3 | 2 | 1 |
| 7 | 15 | 10 | 6 | 3 | 1 |
| 8 | 35 | 20 | 10 | 4 | 1 |
| 9 | 70 | 35 | 15 | 5 | 1 |
| 10 | 126 | 56 | 21 | 6 | 1 |
| 11 | 205 | 79 | 23 | 2 | -4 |
| 12 | 305 | 100 | 21 | -2 | -4 |
| 13 | 420 | 115 | 15 | -6 | -4 |
| 14 | 540 | 120 | 5 | -10 | -4 |
| 15 | 651 | 111 | -9 | -14 | -4 |
| 16 | 735 | 84 | -27 | -18 | -4 |
| 17 | 780 | 45 | -39 | -12 | 6 |
| 18 | 780 | 0 | -45 | -6 | 6 |
| 19 | 735 | -45 | -45 | 0 | 6 |
| 20 | 651 | -84 | -39 | 6 | 6 |
| 21 | 540 | -111 | -27 | 12 | 6 |
| 22 | 420 | -120 | -9 | 18 | 6 |
| 23 | 305 | -115 | 5 | 14 | -4 |
| 24 | 205 | -100 | 15 | 10 | -4 |
| 25 | 126 | -79 | 21 | 6 | -4 |
| 26 | 70 | -56 | 23 | 2 | -4 |
| 27 | 35 | -35 | 21 | -2 | -4 |
| 28 | 15 | -20 | 15 | -6 | -4 |
| 29 | 5 | -10 | 10 | -5 | 1 |
| 30 | 1 | -4 | 6 | -4 | 1 |
| 31 | 0 | -1 | 3 | -3 | 1 |
| 32 | 0 | 0 | 1 | -2 | 1 |
| 33 | 0 | 0 | 0 | -1 | 1 |
| 34 | 0 | 0 | 0 | 0 | 1 |
| 35 | 0 | 0 | 0 | 0 | 0 |
各表の右端の列を見ると分かるように、6個ずつの数値が並んでおり、正負が順に交代するようになっている。一応、これをもって規則性と見なすこととした。
右端の列は第n-1階差にあたる。
この右端の列を抜き出して、6つごとの固まりを表記すると次の通りになる。
| 2 | 1, -1 |
| 3 | 1, -2, 1 |
| 4 | 1, -3, 3, -1 |
| 5 | 1, -4, 6, -4, 1 |
ここまで書けばわかると思うが、二項定理が現れている。
つまり、「nD6で任意の値が出る確率の分子部分は、第n-1階差において二項定理における奇数を正、偶数を負とした数値が6個ずつ並んでいる数列である」と表記できる。
規則性が分かったので、これで式を書くことができる。
式を作る工程は説明するのが面倒なので省く。結局次のようになった。
nD6をロールしたときに出目dが出る確率Pdは、
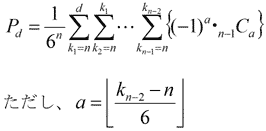
となる。
これが6面ダイスを複数個振ったときの結果である。6個ごとに1つ進むという形式上、床関数を使うことにした。MODを使っても良かったのだけど、どちらにしろリニアな式は得られないのでどちらでも同じだということで結果を直接認識しやすい床関数を選んだ。
ついでに、n面ダイスを振ったときについても考えようと思うが、6面体のときに6になっている部分をnに変えるだけなので、何も考えずにできる。
nDmをロールしたときに出目dが出る確率Pdは、
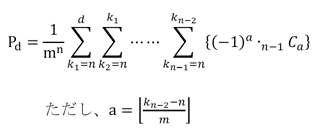
となる。
ちなみに、こいつらシグマとかコンビネーションのせいでこれ以上分解できなかった。
ちゃんと解けたらn→∞のときに正規分布に収束するかを調べたかったのだけど、それどころじゃあなかった。
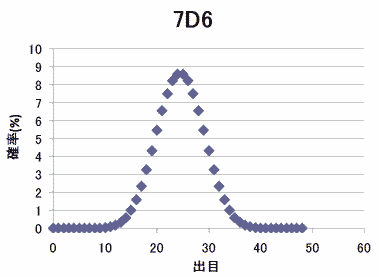
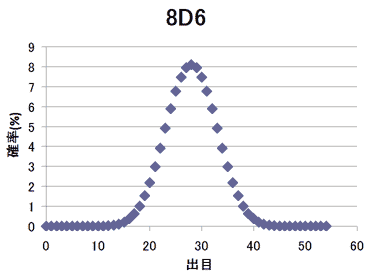
さて、折角一般項が得られたので、7D6と8D6も確率分布を算出しておく。
7D6
| 7 | 1/279936 |
| 8 | 7/279936 |
| 9 | 28/279936 |
| 10 | 84/279936 |
| 11 | 210/279936 |
| 12 | 462/279936 |
| 13 | 917/279936 |
| 14 | 1667/279936 |
| 15 | 2807/279936 |
| 16 | 4417/279936 |
| 17 | 6538/279936 |
| 18 | 9142/279936 |
| 19 | 12117/279936 |
| 20 | 15267/279936 |
| 21 | 18327/279936 |
| 22 | 20993/279936 |
| 23 | 22967/279936 |
| 24 | 24017/279936 |
| 25 | 24017/279936 |
| 26 | 22967/279936 |
| 27 | 20993/279936 |
| 28 | 18327/279936 |
| 29 | 15267/279936 |
| 30 | 12117/279936 |
| 31 | 9142/279936 |
| 32 | 6538/279936 |
| 33 | 4417/279936 |
| 34 | 2807/279936 |
| 35 | 1667/279936 |
| 36 | 917/279936 |
| 37 | 462/279936 |
| 38 | 210/279936 |
| 39 | 84/279936 |
| 40 | 28/279936 |
| 41 | 7/279936 |
| 42 | 1/279936 |
8D6
| 8 | 1/1679616 |
| 9 | 8/1679616 |
| 10 | 36/1679616 |
| 11 | 120/1679616 |
| 12 | 330/1679616 |
| 13 | 792/1679616 |
| 14 | 1708/1679616 |
| 15 | 3368/1679616 |
| 16 | 6147/1679616 |
| 17 | 10480/1679616 |
| 18 | 16808/1679616 |
| 19 | 25488/1679616 |
| 20 | 36688/1679616 |
| 21 | 50288/1679616 |
| 22 | 65808/1679616 |
| 23 | 82384/1679616 |
| 24 | 98813/1679616 |
| 25 | 113688/1679616 |
| 26 | 125588/1679616 |
| 27 | 133288/1679616 |
| 28 | 135954/1679616 |
| 29 | 133288/1679616 |
| 30 | 125588/1679616 |
| 31 | 113688/1679616 |
| 32 | 98813/1679616 |
| 33 | 82384/1679616 |
| 34 | 65808/1679616 |
| 35 | 50288/1679616 |
| 36 | 36688/1679616 |
| 37 | 25488/1679616 |
| 38 | 16808/1679616 |
| 39 | 10480/1679616 |
| 40 | 6147/1679616 |
| 41 | 3368/1679616 |
| 42 | 1708/1679616 |
| 43 | 792/1679616 |
| 44 | 330/1679616 |
| 45 | 120/1679616 |
| 46 | 36/1679616 |
| 47 | 8/1679616 |
| 48 | 1/1679616 |
本当は証明しないといけないのだけどちょっと証明方法が思いつかないので、演繹的に導くだけでnDmの確率は終了とする。二項定理が出てくる原因とかの部分を丁寧に見ていけば道筋は開けそうな気がするのだけど、面倒なので。気が向いたらもう少しまじめに考えてみようと思う。
計算に使ったエクセルファイルはこちら(4.06MB)。
20161017
筋道立てた方法で確率を導きました。
関連エントリー
20161017 複数のダイスを振ったときの確率
20160412 ウタカゼ 判定の達成値
20150807 ドラスレ確率計算
20150722 ドラスレ遊んだよ
20150516 でたとこサーガ 判定の達成値と確率について
20150505 でたとこサーガ遊んだよ
20120929 アサルトエンジン リロールの確率について