ドラスレの確率計算をした。面倒ではあるけど、それほど複雑ではない。ぎりぎりエクセルでも計算出来るけど、サイコロの数が増えると精度が悪くなるというレベル。
ちょっと思考が簡潔に纏まらないので雑な書き方をする。
確率の表記について、Pn,mという確率の書き方をする。Pは確率、nはロールするダイスの数。mは成功数。
まず、1Dの場合。特に何も考えずに各成功数となる組み合わせと、その確率を足し合せれば良いので特に考えることなく求めることが出来る。
P1,-1:m=-1、成功数-1のとき
サイコロを1個振って1が出たときだけなので、
P1,0:m=0、成功数0のとき
サイコロを1個振ったときに2,3が出たとき、及び、6が出て、振り足したサイコロが1だったときの合計なので、
P1,1:m=1、成功数1のとき
サイコロを1個振ったときに4,5が出たとき、及び、6が出て、振り足したサイコロが6→1だったときの合計なので、

P1,2のとき
サイコロを1個振ったときに6→2~5、及び6→6→6→1の合計。

P1,3のとき
サイコロを1個振ったときに6→6→2~5、及び6→6→6→6→1の合計。

P1,nのとき
サイコロを1個振ったときに6がn-1回連続で出た後に2~5がでたとき、および、6がn+1回連続で出た後に1が出たときの合計となる。

以上より、1Dを振ったときの成功数の確率が得られた。
2Dの場合も同じように全てのパターンを書き出していこうかと思ったのだけど、ちょっと面倒なので、考え方と結論を書いて済ませてしまう。
2つのサイコロの合計が目標とする値となる組み合わせが複数ある。例えば目標成功数が2だとすると、2つのサイコロの成功数は(-1,3)(0,2)(1,1)(2,0)(3,-1)の5通りの組み合わせがある。それぞれの確率は、
(-1,3):P1,-1×P1,3
(0,2):P1,0×P1,2
(1,1):P1,1×P1,1
(2,0):P1,2×P1,0
(3,-1):P1,2×P1,-1
となる。この5つの合計が成功数2の場合、つまりP2,2となる。これをまとめると次の様になる。

これを2D全体に敷衍して考えると、P2,mは次のようにあらわすことが出来る。

3D以降についてだが、全てのダイスの組み合わせを考えるとダイスの増加に対して等比級数的に組み合わせが増えてしまうので一工夫いる。
n個のダイスを振ったときを考える場合、n-1個のダイスを振ったときの成功数と1個のダイスを振ったときの成功数を足して目標の成功数となる組み合わせを足し合せることで確率を得ることが出来る。
従って、n個のサイコロを振って成功数mとなる組み合わせは、(-n+1,m+n-1)(-n+2,m+n-2)・・・・・・(m,0)(m+1,-1)となる。これを数式で表記すると、
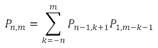
となる。
これで確率一覧表を作ることができるのだけど、エクセルで書くのは結構大変。繰り返し計算が必要なので、1つのセルを埋めるために2次元のマトリックスで解かなければならない。サブルーチンを使いたくなるのだけど、エクセルにはサブルーチンは関数として実装されていないためマクロとかVBAとかいったよく分からないものを使わなければならないので、諦めてセル1つ1つを地道に計算して埋めた。
結果、次の様な表が得られた。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| -13 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 |
| -12 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 |
| -11 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 |
| -10 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 1.65E-08 |
| -9 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 9.92E-08 | 3.58E-07 |
| -8 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 5.95E-07 | 1.93E-06 | 3.83E-06 |
| -7 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 3.57E-06 | 1.03E-05 | 1.86E-05 | 2.68E-05 |
| -6 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 2.14E-05 | 5.42E-05 | 8.79E-05 | 1.17E-04 | 1.38E-04 |
| -5 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 1.29E-04 | 2.79E-04 | 4.03E-04 | 4.89E-04 | 5.39E-04 | 5.60E-04 |
| -4 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 7.72E-04 | 1.39E-03 | 1.77E-03 | 1.95E-03 | 1.99E-03 | 1.94E-03 | 1.84E-03 |
| -3 | 0.00E+00 | 0.00E+00 | 4.63E-03 | 6.69E-03 | 7.34E-03 | 7.27E-03 | 6.86E-03 | 6.29E-03 | 5.68E-03 | 5.08E-03 |
| -2 | 0.00E+00 | 2.78E-02 | 3.01E-02 | 2.80E-02 | 2.48E-02 | 2.16E-02 | 1.87E-02 | 1.61E-02 | 1.38E-02 | 1.19E-02 |
| -1 | 1.67E-01 | 1.20E-01 | 9.34E-02 | 7.41E-02 | 6.00E-02 | 4.92E-02 | 4.08E-02 | 3.40E-02 | 2.86E-02 | 2.42E-02 |
| 0 | 3.61E-01 | 2.43E-01 | 1.78E-01 | 1.38E-01 | 1.10E-01 | 8.91E-02 | 7.33E-02 | 6.08E-02 | 5.09E-02 | 4.28E-02 |
| 1 | 3.38E-01 | 2.81E-01 | 2.31E-01 | 1.90E-01 | 1.58E-01 | 1.31E-01 | 1.10E-01 | 9.29E-02 | 7.86E-02 | 6.68E-02 |
| 2 | 1.12E-01 | 2.01E-01 | 2.12E-01 | 2.00E-01 | 1.81E-01 | 1.60E-01 | 1.40E-01 | 1.23E-01 | 1.07E-01 | 9.26E-02 |
| 3 | 1.86E-02 | 9.01E-02 | 1.42E-01 | 1.64E-01 | 1.69E-01 | 1.64E-01 | 1.53E-01 | 1.41E-01 | 1.27E-01 | 1.14E-01 |
| 4 | 3.11E-03 | 2.75E-02 | 7.01E-02 | 1.06E-01 | 1.29E-01 | 1.41E-01 | 1.44E-01 | 1.42E-01 | 1.35E-01 | 1.27E-01 |
| 5 | 5.18E-04 | 6.68E-03 | 2.68E-02 | 5.54E-02 | 8.26E-02 | 1.04E-01 | 1.18E-01 | 1.25E-01 | 1.28E-01 | 1.26E-01 |
| 6 | 8.63E-05 | 1.46E-03 | 8.39E-03 | 2.37E-02 | 4.44E-02 | 6.57E-02 | 8.42E-02 | 9.86E-02 | 1.08E-01 | 1.14E-01 |
| 7 | 1.44E-05 | 3.01E-04 | 2.29E-03 | 8.63E-03 | 2.04E-02 | 3.60E-02 | 5.29E-02 | 6.89E-02 | 8.26E-02 | 9.32E-02 |
| 8 | 2.40E-06 | 5.99E-05 | 5.68E-04 | 2.75E-03 | 8.17E-03 | 1.74E-02 | 2.95E-02 | 4.32E-02 | 5.68E-02 | 6.93E-02 |
| 9 | 4.00E-07 | 1.16E-05 | 1.32E-04 | 7.92E-04 | 2.90E-03 | 7.42E-03 | 1.47E-02 | 2.43E-02 | 3.55E-02 | 4.71E-02 |
| 10 | 6.66E-08 | 2.20E-06 | 2.94E-05 | 2.11E-04 | 9.36E-04 | 2.86E-03 | 6.59E-03 | 1.24E-02 | 2.02E-02 | 2.93E-02 |
| 11 | 1.11E-08 | 4.11E-07 | 6.30E-06 | 5.30E-05 | 2.78E-04 | 1.00E-03 | 2.69E-03 | 5.78E-03 | 1.05E-02 | 1.68E-02 |
| 12 | 1.85E-09 | 7.60E-08 | 1.31E-06 | 1.27E-05 | 7.76E-05 | 3.26E-04 | 1.01E-03 | 2.47E-03 | 5.03E-03 | 8.89E-03 |
| 13 | 3.08E-10 | 1.39E-08 | 2.68E-07 | 2.93E-06 | 2.05E-05 | 9.90E-05 | 3.53E-04 | 9.80E-04 | 2.23E-03 | 4.21E-03 |
| 14 | 5.14E-11 | 2.53E-09 | 5.37E-08 | 6.56E-07 | 5.18E-06 | 2.84E-05 | 1.15E-04 | 3.62E-04 | 9.02E-04 | 1.60E-03 |
| 15 | 8.57E-12 | 4.55E-10 | 1.06E-08 | 1.43E-07 | 1.26E-06 | 7.79E-06 | 3.55E-05 | 1.24E-04 | 3.05E-04 | 3.91E-04 |
| 16 | 1.43E-12 | 8.17E-11 | 2.06E-09 | 3.05E-08 | 2.97E-07 | 2.05E-06 | 1.03E-05 | 3.69E-05 | 7.10E-05 | 6.52E-05 |
| 17 | 2.38E-13 | 1.46E-11 | 3.97E-10 | 6.39E-09 | 6.83E-08 | 5.16E-07 | 2.73E-06 | 8.12E-06 | 1.18E-05 | 1.09E-05 |
| 18 | 3.97E-14 | 2.59E-12 | 7.57E-11 | 1.32E-09 | 1.53E-08 | 1.22E-07 | 5.68E-07 | 1.35E-06 | 1.97E-06 | 1.81E-06 |
| 19 | 6.61E-15 | 4.58E-13 | 1.43E-11 | 2.67E-10 | 3.27E-09 | 2.41E-08 | 9.46E-08 | 2.26E-07 | 3.29E-07 | 3.02E-07 |
| 20 | 1.10E-15 | 8.07E-14 | 2.68E-12 | 5.27E-11 | 6.18E-10 | 4.01E-09 | 1.58E-08 | 3.76E-08 | 5.48E-08 | 5.03E-08 |
| 21 | 1.84E-16 | 1.41E-14 | 4.95E-13 | 9.58E-12 | 1.03E-10 | 6.68E-10 | 2.63E-09 | 6.27E-09 | 9.13E-09 | 8.38E-09 |
| 22 | 3.06E-17 | 2.40E-15 | 8.69E-14 | 1.60E-12 | 1.72E-11 | 1.11E-10 | 4.38E-10 | 1.04E-09 | 1.52E-09 | |
| 23 | 5.10E-18 | 3.90E-16 | 1.44E-14 | 2.66E-13 | 2.86E-12 | 1.86E-11 | 7.30E-11 | 1.74E-10 | ||
| 24 | 8.50E-19 | 6.16E-17 | 2.39E-15 | 4.43E-14 | 4.77E-13 | 3.09E-12 | 1.22E-11 | |||
| 25 | 1.42E-19 | 9.70E-18 | 3.93E-16 | 7.38E-15 | 7.95E-14 | 5.16E-13 | ||||
| 26 | 2.36E-20 | 1.52E-18 | 6.44E-17 | 1.22E-15 | 1.32E-14 | |||||
| 27 | 3.94E-21 | 2.38E-19 | 1.05E-17 | 2.03E-16 | ||||||
| 28 | 6.56E-22 | 3.70E-20 | 1.69E-18 | |||||||
| 29 | 1.09E-22 | 5.72E-21 | ||||||||
| 30 | 1.82E-23 |
紙幅の都合で10Dまで。また、12D以降を求めようとすると誤差が大きくなってしまい見苦しい。誤差については計算ミスかどうかを調べるのも大変なので放置しておく。
これをグラフにすると次のようになる。

ダイスの数と目標成功数と成功率の関係は積分値として描くことが出来る。
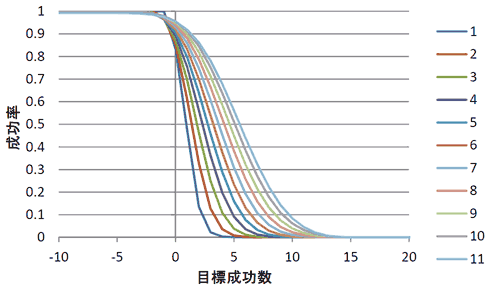
11Dでは積算値が99.2%とすでにだいぶ誤差が大きくなっており、少し低くでている。
以上でドラスレ確率計算は終了とする。
折角なので、例によって計算に使ったエクセルファイルをアップしておく。
ドラスレ確率計算.xls
関連エントリー
20150412 ウタカゼ 判定の達成値
20150722 ドラスレ遊んだよ
20150516 でたとこサーガ 判定の達成値と確率について
20150505 でたとこサーガ遊んだよ
20140531 複数のダイスを振ったときの出目の合計が任意の値となる確率
20120929 アサルトエンジン リロールの確率について