分散液の液中に含まれる塩を除去するのには透析という手法がよく取られる。世間一般では人工透析という言葉で知られているが、原理は濾過と同じで一定以上のサイズの粒子が通らないフィルターで塩や微小粒子を除去する。この透析膜を糸状の細いチューブにしたものを中空糸膜と呼ぶ。中空糸膜を束にして効率よく透析できるようにした装置がダイアライザーである。ダイアライザーは人工透析用のモジュールがメイン(というか検索してもこれしか出てこない)だけど、医療用以外で使ってははいけない法はない。この中を圧力をかけて液を通すことで不要な成分を除去することができる。
透析はやってることは濾過と同じであり、限外濾過とも呼ばれる。進めるに従い液量が減って濾過されない粒子が濃縮されていく。ダイアライザーによる透析は常に液を流し続けなければならないので、濃縮しすぎると都合が悪い。そこで、一定の濃度を保つように加水する。
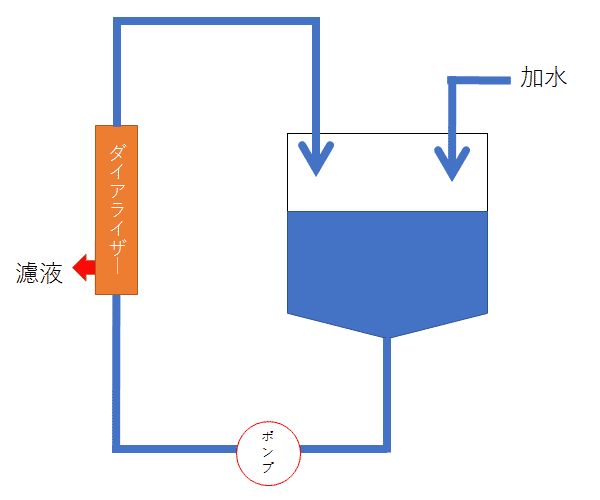
こうして図のような実験装置を考える。実験する以上は透析によって液をどこまできれいにするかという目標を設定しなければならない。そして、どの程度透析したら目標値に至るかを事前に見積もっておきたくなるものである。というのが当エントリーの本題。
計算のために話をモデル化すると、溶液を除去しながら除去したのと同じ量の溶媒を加えるという設定に置き換えられる。ここには溶媒と塩しか出てこず、前後で変化のない膜とか膜を通らない粒子は考慮する必要がない。
いきなり解を求めて難しい計算をするのも分りづらいので、分りやすいモデルから目標に近づけていく。初期濃度をC0、液量10Lとして、10L加水するときうモデルを考える。
・1度で行う(10L加水して10L除去する)
・2度で行う(5L加水して5L除去を2回)
1度目:
2度目:
・3度で行う(10/3L加水して10/3L除去を3回)
1度目:
2度目: 3度目:
・4度で行う(10/4L加水して10/4L除去を3回)
1度目:
4度目:
・n度で行う(10/nL加水して10/nL除去をn回)
n度目:
ここで、n→∞としたときに濾過しながら加水をし続けるという状況を作ることができる。
これは複利計算を無限に分割するとネイピア数になる[1]のと同じだと直覚するので、この極限の式をどうにかコネクリ回して公式に当て嵌める。
使う公式はネイピア数の出てくるやつ。
#################################
# #
# #
# #
#################################
次のように式変形して公式に合わせる。
となる。
というわけで、元の液量と同じ量だけ透析・加水すると濃度は1/e倍になるという結果である。透析の目標濃度をCendとすると、次のように元の液量の倍数で加水量を表すことができる。
実際に透析してみると、これがただの皮算用だということが分かる。全然目標濃度に至らないのである。
分散液中の粒子と塩は大抵電気的に中性ではなく、静電的に引かれ合うので、塩はあまり自由ではないからである。
上の式を適用すれば、できるだけ濃縮して液量が少なくなればより効率よく透析できることになるが、濃度が高ければ高いほど粒子と塩の距離が近づいて静電引力が強くなるので系から抜けて行きづらくなる。
また、系の濃度が常に均一であるという前提で表現しているが、実際は濾過膜で濾液が排出される部分で濃度が高く、加水する部分で濃度が低いという濃度の偏りがあり、とても均一とは言えない条件である。
これら部分を計算できるようにするのはちょっと難しそう、というか考え方がぱっと思いつかないのでやらない。今後なにか思いついたら続きを書くかもしれないけど、これまでの傾向から言ってこの手の続きの話はただ複雑化するだけで碌なことがないので、気が乗らない。
とりあえず、今回の皮算用では透析に最低限必要な加水量を求めたということにしておく。
それにしても、はてなブログでは一応MathJaxを使うことができるとはいえ、表示がいまいち汚いし、できないことが色々あって結構不便。table属性で数式を囲うことさえもできなかったので、原始時代のFORTRANみたいな表記をさせてもらった。有料会員になって毎月使用料を払えば普通のHTMLと同じように書くことができるそうなので、きれいに書きたかったら金払えってことなのだろう。
参考文献
[1]【数列】連続複利とネイピア数 ”e”, 大人が学び直す数学