以前、5×5の魔方陣の話で対称性を考慮することで計算速度が速くなるという提案をした。以下のように書いている。
| この筑波大で行ったアルゴリズムを見ると、対称性に対する評価が抜けているので、これを入れると計算量がだいぶ減らせる。例えば、左上の端に入れたことのある数値が残りの角地に入った時、それは既に計算済みとするだけで最大1/4に減らせる。更に、裏返した形を回避するために、左上が同じで右上に入れたことのある数値が左下にきたときを同じと見なすことで更に1/2にすることができる。この2点を実装するだけで計算量が最大1/8になる。 |
魔方陣のパターン算出の具体的な計算方法を何となく思いついたので、ここに書いておこうと思う。これから魔方陣の算出をしようと考える方には参考になるかも知れない。あるいは、先のエントリーから1年経っており、全くこの辺りのリサーチをしていないので世間の動向を知らず、もしかしたらとっくに誰かがやっているかも知れない。この提言により1/8は無理だけど、それに近い時間の短縮ができるんじゃないかな。
一応、3×3の魔方陣を説明した際も対称性には言及している。
| 一番上と少し違うが、左右に線対称の形にしてやれば同じになる。「本質的に」1種類しかないというわけ。 |
この「本質的に」という言葉で対称性を記述している。この点は魔方陣を使う必要もないで、以前ナイトウィザードで描いたキャラのイラストで説明する。

これを回転&裏返すことで以下のように8つのイラストを作ることができる。
| E | C4 | C42 | C43 |
 |  |  |  |
| σv | σvC4 | σvC42 | σvC43 |
 |  |  |  |
裏返してみると、やっぱりチョット拙いなあというのが分かってしまう。まあ、イラストはTRPGでキャラクターシートに描ければいいや、という程度の認識しか持っていないので特に釈明することもない。
C4とかσvとかいう記号は群論で使うもの。一応、識別できるように記号を振ったが、今回は特に用はないので気にしなくて問題はない。
この8つのイラストを全て同じものであると見做して同じものを計算しようとた時にそれを飛ばすということで、計算時間を1/8以上に短縮する、というのが肝。
下に示すように正方形を8つに間切ってやり、その内の1つのピース(青い線で囲ったもの)に目をつける。

この直角二等辺三角形が8つ集まると正方形になることはわかると思う。上に描いた回転操作などを加えた8つの本質的に同じイラストと、この8つに間切った正方形を重ねると、青い線で囲った部分は全部異なった絵柄があることがわかる。
| E | C4 | C42 | C43 |
 |  |  |  |
| σv | σvC4 | σvC42 | σvC43 |
 |  |  | 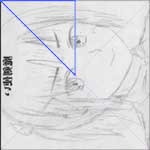 |
ちょっと迂遠で分かりづらいのだけど、この青で囲った三角形を見張っておくことで本質的に同じ8種類の図形を1種類に収束することができるのではないかと考えたわけである。
この考えを魔方陣に転化するにあたって思考の飛躍があるのだけど、この思考の変遷は直感に依っているところもあり上手く伝える言葉を持たないので、最後まで読んで薄い繋がりを認識してもらうしかない。
青い線で囲った部分を魔方陣に転写すると次の●で示した部分になる。
| ● | ● | ● | ||
| ● | ● | |||
| ● | ||||
25箇所を見る必要があったのが、実は6箇所でよかったということになる。上で1/8とか言ってたのは大分大げさな話で、実は6/25だったということ。それでも約1/4なので計算の効率化という点ではかなりの効果を期待できる。
具体的に何をしたらよいかというと、ある特定の数字を取り上げて考える。例えば"1"を取り上げて考える。上の図で●で示した部分以外に1が入る組み合わせに対して必ず●で示したマスに1が入る組み合わせが存在するので、●以外の部分に1が入る場合は計算する必要がない。
次の図は5×5の魔方陣を計算するときの数字を当てる順番だが、

ここで、①②③⑧⑨⑪番目に1が入ったときだけ計算すれば良いということになる。
メインとなる考えは以上。このやり方だと後処理が必要になる。というのはこれは6/25ということから分かる通り、本質的に異なった魔方陣だけを集めたわけではないということ。6/25 - 1/8 = 23/200、つまり1割強の本質的に同じ魔方陣が混ざっていることになる。最終的に解を出すには、全て集めるか、綺麗に分離するか、というどちらかにしなければならない。
前者については割と簡単で、解を見つけた度に8種類の本質的に同じものを計算し、規則に則った順で書き出していけば良い。全く同じ魔方陣があった場合は、書き出すべきアドレスにすでに同じものがあるのでそれとわかる。
後者については悩ましいところだが、③については全て書き出されており、①②⑨⑪については隣のマスを共有する部分と重なった解があり、⑧は本質的にこれしかない。そんなわけで、③は8種類、①②⑨⑪は2種類の本質的に同じ魔方陣があるので、見つけ出して潰さなければならない。見つけ出すと言っても、本質的に同じものというのは対象操作を行うことによって求めることができる上に、どの操作を行えば求まるかもその位置から明らかである。⑨⑪であれば左右を反転させるσv、①②であれば左右を反転させて270度回転するσvC43、③は8種類勿論全ての操作である。
この2つのどちらが速いかはやってみないと分からないけど、個人的には出力するデータの少ない後者を推す。
そんなわけで、魔方陣の計算の効率化の話でした。対称性を利用して6/25まで計算回数を減らすことができるというのが今回の話題だけど、もっと洗練することで1/8に近づけることはできるのかもしれない。ちなみに、5×5の魔方陣で説明したけど、もちろんもっと大きな魔方陣でも同様に計算を効率化することができる。
関連エントリー
20140308 高校生が筑波大のスパコンを使い、「5×5魔方陣」を解明
20110530 3×3の魔方陣