ダブルクロス目標値と成功確率

　ダブルクロスは判定方法が独特なので、遊ぶ度に色々と計算してやろうっていう気になる。
　以前、ダブルクロスの判定の期待値について計算したことがある。このときは、ダイスを1個しか振らないという極めて限定的な場合で検討した。今回は、期待値ではなく目標値に対する成功確率、それもクリティカル値、ダイス数も含めてを求めてみた。
　判定の際にクリティカル値を下げるか、ダイスを増やすかの選択で役に立つかもしれない。今回は期待値は求めないが、後述のようにそれに近い値は一応出している。もしかしたら、ここから期待値に発展させることもできるかもしれないけど、取り敢えず今回は期待値は検討しない。

　判定は以下の通り^[1]。

1. 複数個の10面ダイスを振る。
2. クリティカル値以上の出目のダイスがなかった場合は最も高い値を達成値として採用。クリティカル値以上のダイスは達成値を10として再度振り足す。
3. 2で振り足したダイスがクリティカル値以上の場合は達成地にさらに10を足して振り足す。すべてクリティカル値未満だった場合は最も高い値を達成値として採用。
4. クリティカル値以上の目がでなくなるまで繰り返す。

　説明が分かりにくいかもしれないけど、ダブルクロスを遊んだことのない人がこんなエントリーを読みに来るとも思えないので、テキトーなままにしておく。説明が理解できないけど、どうしても知りたいという方はルールブックを読むとかセッションに参加するとかしてもらうとよいと思う。

　まず、ダブルクロスの判定の際、達成値を求めるためにダイスの出目に技能レベルと修正を足す。この部分を考慮すると無意味に煩雑になるので、前提として技能レベルや修正はないものとする。これらを加味したい場合は目標値をその分引いてやれば良いので、敢えて複雑にする必要はないということである。
　目標値、クリティカル値、ダイスの数と確率を求めるための前提となる変数が3つあるので結構複雑になるのは目に見えている。最後には割と単純な式で表されるのでその点は安心してもらってよい。しかし、最終結果として4つの値を一つのグラフで表すのは無理があるので複数のグラフを表示することになる。この部分は、最後に上げるエクセルファイルを落としてもらって好きなように値を変更したら欲しいグラフが表示されるようになっているので、好きにしてもらったら良いと思う。
　計算する上で複雑になる要因としてダイスの数がある。前回は1Dという条件に限定したのはこの部分が原因である。この点をクリアするに当たって、ダイスを1つずつ振っていくという考察をした。確率の基本は(成功する場合の数/起こりうる場合の総数)を考える^[2]。期待値を考える場合は無限級数をクリアしないといけないが、確率だけであれば、成功するか失敗するかの2択となるので幾分楽である。
　ダイスを1個を振ったときの確率であれば、何回のクリティカルが必要でその後いくつの目を出せばよいのかはっきりしているので簡単に求められる。例えば、目標値35でクリティカル10だとすれば、3回クリティカルを出した後に5以上を出せば良いので、 ${ \frac{1}{10} \cdot \frac{1}{10} \cdot \frac{1}{10} \cdot \frac{10-4}{10} = \frac{6}{10000} }$ と簡単に求められる。勿論この判定を成功させるのは簡単ではない。
　ここで、ダイスを増やすとどうなるかという話になる。複数のダイスを振る場合は普通はすべてのダイスを手のひらに乗せて振る。1個ずつ振ると後から振ったダイスが既に振ったダイスに当たって出目を変えてしまうことがあるから。これを敢えてやるとパワーダイスと呼ばれるイカサマになる。しかし、数学の計算上では先に振ったダイスの目など記録しておけば良いことだし、そもそも紙の上で計算するだけであって実際にダイスを振るわけではない。そんなわけで、確率を求める考え方として、1個目のダイスで成功したら良し、成功しなかったら次のダイスを振るという考え方をした。
　計算の手続きとしては、1Dのときの成功確率を求めて、失敗した場合は失敗した確率に1Dの成功確率を掛けた値を足すという手続きで降るダイスの数を増やすようにした。
　例えば、目標値8として考えると1Dでは ${ \frac{3}{10} }$ 、2Dでは ${ \frac{3}{10} + \frac{7}{10} \cdot \frac{3}{10} }$ 、3Dでは ${ \frac{3}{10} + \frac{7}{10} \cdot \frac{3}{10} + \frac{7}{10} \cdot \frac{7}{10} \cdot \frac{3}{10} }$ となる。面倒なんで計算はしない。図に描くと次のようにサイコロを増やすと全事象から成功領域が増えていくということになる。

　それはそうと、端っこから例示して帰納していこう。

　以下の意味で記号を使う。
C：クリティカル値, 2以上の値を取る。ただし、11以上の場合は11とする。
T：目標値
d：ダイスの数
P_d：d個のダイスを振ったときの成功確率
P：ダイス1個のときの確率, P = P₁
n：適当な整数

クリティカル値10のとき(C=10)
・目標値T=1～10
$P = \frac{11-T}{10}$
・目標値T=11～20
$P = \frac{1}{10} \cdot \frac{21-T}{10}$
・目標値T=21～30
$P = \left( \frac{1}{10} \right)^2 \cdot \frac{31-T}{10}$

・目標値T=10n+1～10n+10
$P = \left( \frac{1}{10} \right)^n \cdot \frac{10n+11-T}{10}$

クリティカル値9のとき(C=9)
・目標値T=1～8
$P = \frac{11-T}{10}$
・目標値T=9～10
$P = \frac{2}{10}$
・目標値T=11～18
$P = \frac{2}{10} \cdot \frac{21-T}{10}$
・目標値T=19～20
$P = \left( \frac{2}{10} \right)^2$
・目標値T=21～28
$P = \left( \frac{2}{10} \right)^2 \cdot \frac{31-T}{10}$
・目標値T=29～30
$P = \left( \frac{2}{10} \right)^3$

・目標値T=10n+1～10n+8
$P = \left( \frac{2}{10} \right)^n \cdot \frac{10n+11-T}{10}$
・目標値T=10n+9～10n+10
$P = \left( \frac{2}{10} \right)^{n+1}$

クリティカル値Cのとき
・目標値T=1～C
$P = \frac{11-T}{10}$
・目標値T=C+1～10
$P = \frac{11-C}{10}$
・目標値T=11～10+C
$P = \frac{11-C}{10} \cdot \frac{21-T}{10}$
・目標値T=11+C～20
$P = \left( \frac{11-C}{10} \right)^{2}$
・目標値T=21～20+C
$P = \left( \frac{11-C}{10} \right)^{2} \cdot \frac{31-T}{10}$
・目標値T=21+C～30
$P = \left( \frac{11-C}{10} \right)^{3}$

・目標値T=10n+1～10n+C
$P = \left( \frac{11-C}{10} \right)^{n} \cdot \frac{10n+11-T}{10}$
・目標値T=10n+1+C～10n+10
$P = \left( \frac{11-C}{10} \right)^{n+1}$

以上より、Pの一般項は
・目標値T=10n+1～10n+Cの場合、
$P = \left( \frac{11-C}{10} \right)^{n} \cdot \frac{10n+11-T}{10}$
・目標値T=10n+1+C～10n+10の場合
$P = \left( \frac{11-C}{10} \right)^{n+1}$
となる。
　なお、クリティカル値11の場合を省いたけど、T=1～10の部分はC=10と同じだし、T>10では全て0になるのでこれでよい。
　ルールの構造上どうしてもクリティカル値前後で扱いが変わってしまうので場合分けせずには表記できない。場合分けしたが、目標値がCのところではどちらの式を使っても同じになる。

　引き続き、今度はダイスを増やしていく。
　上で説明したことを式にすると、P_n+1 = P_n + (1-P_n)Pという漸化式になる。
　基本的に、この数列を解くことになる。

ダイス2つのとき(d=2)
$P_2 = P + (1-P)P \\ \hspace{ 15pt }= 2P - P^2$
ダイス3つのとき(d=3)
$P_3 = 2P - P^2 + {1-(2P-P^2)}P \\ \hspace{ 15pt }= 3P - 3P^2 + P^3$
ダイス4つのとき(d=4)
$P_4 = 3P - 3P^2 + P^3+(1- 3P + 3P^2 - P^3)P \\ \hspace{ 15pt }= 4P - 6P^2 + 3P^3 - P^4$
ここまで書き出してみると、パスカルの三角形の一番左の項がないものであることに気付く。
　パスカルの三角形では、次の段は同じ段を一つ横にずらしたものを足すと次の段となる構造をしている。上で示した漸化式P_d+1 = P_d + P -P_d・Pをみると、元のP_dが元の段を表しており、-P_d・Pが一つ横にずらしたものに当たる。Pを掛けているので次数が一つ増えるのである。そして、P¹の項は+Pによって1ずつ増える。こうして、左端の抜けたパスカルの三角形が現れる。

　本当はちゃんと証明しないといけないけど、論文を書いてるわけではないのでこれで済ます。
　さて、パスカルの三角形が現れたということは二項定理で示せるはずである。次の公式が二項定理である。
$\left( a + b \right) ^n = \sum_{ k = 0 }^{ n } {}_n C_k a^{n-k} b^k$
　これを使ってP_dの一般項を表す。一番左の項がないということはk=0となるP⁰の項が消えるということで、k=1から総和を始めれば良い。
$P_d = {}_{d} C_1 P - {}_{d} C_2 P^2 + {}_{d} C_3 P^3 + \cdots + (-1)^{d} {}_{d} C_{d} P^{d} \\ \displaystyle \hspace{ 15pt } = \sum_{ k = 1 }^{ d } (-1)^{k+1} {}_{d} C_{k} P^k$
　以上で、成功確率の一般項を示すことができる。

ダブルクロスにおいて判定の成功確率は次のようになる。
$P_d = \sum_{ k = 1 }^{ d } (-1)^{k+1} {}_{d} C_{k} P^k$
　Pについて
・目標値T=10n+1～10n+Cの場合、
$P = \left( \frac{11-C}{10} \right)^{n} \cdot \frac{10n+11-T}{10}$
・目標値T=10n+1+C～10n+10の場合
$P = \left( \frac{11-C}{10} \right)^{n+1}$

　ファンブルがカウントされてないけど、目標値1のときにしか影響がないので、無視した。下記に示すエクセルではファンブルもカウントしてるので安心してほしい。

　実際のところ、この計算は手続きが極めて簡便で判定の最中に咄嗟の判断に供せられるかというと、相当な計算能力が備わっていないと難しいんじゃないかと思う。プロペラオペラのクロトみたいな計算が得意な連中には役立つかもしれない。
　こういうときに役立つのがグラフである。結果を全部図示してしまえば大体この辺りであると目測がつく。
　ところで変数が4つあるので1枚のグラフで表すのは簡単ではない。やって出来ないことはないだろうけど、実際にそういうグラフを作ったところで見る人が理解できなければ意味がない。そこで、クリティカル値ごとに別のグラフを作ることにした。
　横軸を目標値、縦軸を成功確率とし、1～10, 15, 20, 30, 40, 50個のダイスを振ったときの結果をそれぞれ並べた。クリティカル値については別のセルで入力するようにした。目標値については、実はダブルクロスがどれくらいまで設定するゲームなのかよく知らないので、500くらいまであればいいかなと思って設定した。この所為でファイルサイズがちょっと大きくなった。
・DX確率.xlsx
　次に示す感じのグラフとなっている。代表的なクリティカル値として10, 7, 5, 2を上げる。

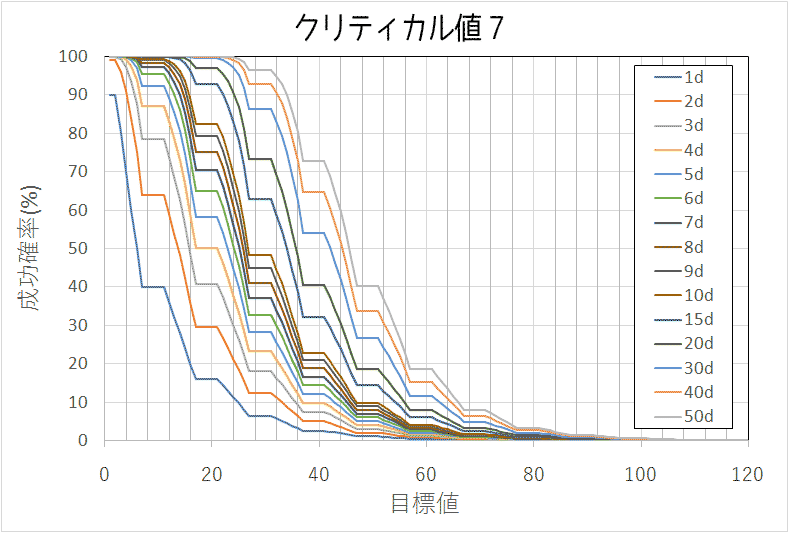
期待値について
　このグラフからは期待値は分からない。期待値が分かると判定前に選択するオプションの見立てが出来て便利である。期待値はないが、50%の確率で成功する目標値というのは分かる。ここでは50%成功率と表記する。中央値と近い概念だけど、中央値とも異なるので50%成功率と呼ぶ。
　正規分布となるものであれば期待値は50%成功率と一致するはずだけど、こういう不連続なグラフでは期待できない。とはいえ、それほど大きく違ってくるとも思えないので、期待値の代わりに使うのも悪くないと思う。次のようになる。

　一応、縦軸を100までとしたものと450までとしたものを上げておく。

参考文献
　[1]矢野俊作 F.E.A.R., ダブルクロス THE 3RD EDITION ルールブック1, 富士見書房(2009)
　[2]確率の定義(魚拓), KIT数学ナビゲーション

関連エントリー
　20181123　ダブルクロス　判定の期待値