ナスフラスコの形を数式で表す

　ナス型フラスコというフラスコがある。短縮してナスフラとか呼ぶのだけど、ロータリーエバポレーターで減圧濃縮するのに都合の良い形状をしている。


　エバポレーターで濃縮する際に、フラスコを回転させることによってフラスコ壁面に薄い液膜を形成させるため、液体の表面積が増加するので蒸発の効率が高まる。
　エバポレーターにナスフラを設置した際に、ジョイントを回転させてフラスコの角度を変えることができる。実験していて常々思うのはこのジョイントはどの角度のときに最も効率よく蒸発させることができるのだろうかということ。一つ計算してやろうと思った。
　思ったのは良いのだけど、少し計算量が多そうなので取り敢えず今回は第一歩としてフラスコの形を数式で表すということを試みることにした。
　ナスフラの形状についてだけど、画像を検索するとメーカーによって少しずつ形状が異なっていることがわかる。普段自分が使っているものが一番よいのだけど、できるだけ単純な形の方が扱いやすい。そこで目を付けたのが石英ガラス製品ドットコムに掲載されているフラスコ。なんと、寸法まで付けてくれており、色々便利だ。

　ナスフラは回転体の形状をしているので、上図の左右どちらか片側の輪郭線を描くことができれば記述したことになる。折角寸法が分かることだしモデルにするフラスコを選ぼう。テキトーに500mlのフラスコにしてみる。石英ガラス製品ドットコム
のページにある製品番号1102-05というものにする。
　共通摺の部分はどうせ使わないのでないものとしよう。すると、ナスフラの形状は直線と円で記述することができる。下図のようにフラスコを横にして第一象限でグラフを描けるように配置して、この形状に合う直線と円を描くことにする。

　まず、底の球状の部分について、球の半径が51なので、中心がx=160-51=109の位置に来る。従って、(x-109)²+y²=51²となる。円は第一象限でしか使わないので後の計算を楽にするために、y=(51²-(x-109)²)^0.5としておく。
　次に、点(0,12)を通ってこの円と接する直線の方程式を求める。
　直線の方程式をy=ax+12として、このaの値を求めれば良い。
　直線から円の式を引いた値が0になるaが1つだけになるとき(重解)、直線と円が接するので、この2つを引いてやれば良い。

　ここまで書いておいて何だけど、どういうわけか上手く計算ができないので方針転換。アプローチを間違えたかな。図形を解いて直線の傾きを求めることにした。
　次の図のように2つの直角三角形に分解して角度を求める。


　三角形①は2辺とその間の角が分かっているので残りの部分も確定する。三平方の定理より斜辺の長さは(12²+109²)^0.5となる。この斜辺は三角形②と共有しているので三角形②も2辺と角1つが決まり、残りの要素も判明する。残りの辺の長さは(12²+109²-51²)^0.5である。今知りたいのは三角形②の残りの辺の傾きである。図のように三角形①②の角をそれぞれα、βとすると、三角形②の残りの辺のx軸となす角度はβ-αとなる。α、βの角度はそれぞれ、α=tan^-1(12/109)、β=tan^-151/(12²+109²-51²)^0.5である。これらを引くことでβ-αは求まる。また、直線の方程式において傾きは、直線の角度の正接に等しいので、tan(β-α) = tan(tan^-151/(12²+109²-51²)^0.5-tan^-1(12/109))となる。接点は、(12²+109²-51²)^0.5cos(β-α)となる。
　以上より、だいぶ力尽くなのだけど、直線の方程式を求めることができた。

　これで、直線と円の方程式が得られた。直線と円の接点で場合分けして解く。

　このグラフをx軸中心で回転するとナスフラの形が得られる。
　エクセルで描くと次のようになった。

　この数値をそれぞれ文字に置き換えることで一般解とすることができる。
　上の図から、高さ：L、幅：D、口径：Jとすると、この場合L=160、D=102、J=24であり、これらを使って式を書き換える。
0≦x≦接点のとき

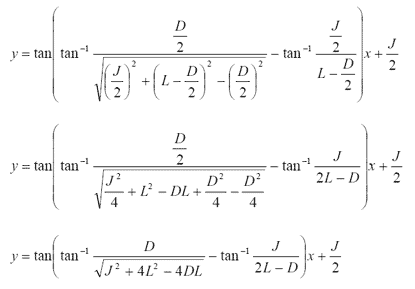
接点≦x≦Lのとき

接点

以上より、一般解が得られた。

　折角なので、3次元で表記しておこう。とはいっても、x軸を中心に回転させるだけなので、x軸からの距離が上のyとなる点の集合を描けば良い。ということは、xが0～Lのときにx軸を中心とする無数のy-z平面上の円を重ねあわせることで表記できる。左辺はy²+z²で、右辺が上の式の2乗である。改めて書くと以下のようになる。

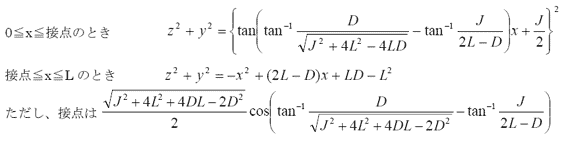
　図を書くのに使ったエクセルファイルも上げておく。
DL:ナスフラ.xls